真愛方程式速解

真愛方程式速解

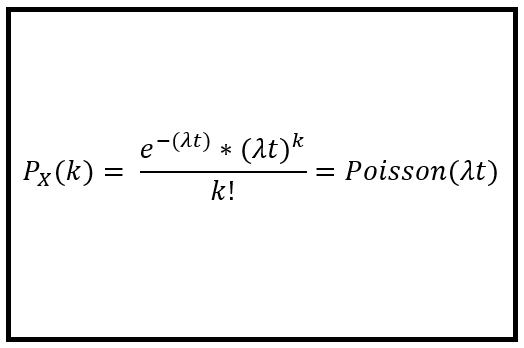
數學家彼得巴克斯（Peter Backus）曾在論文《我為什麼沒有女朋友》中運用「德瑞克方程式」（Drake equation）計算出遇到真愛的機率約是二十八點五萬分之一。

1/285000是真愛率，366是我目前tinder的配對人數。

若將每次配對皆視為獨立成敗試驗，直到遇到真愛才算成功，定義所需的試驗次數X為隨機變數，則X～Geo(p=1/285000)，P(X≤366)= Σ [(1/285000)^1][(284999/285000) ^x-1]= 0.00295282802162，也就是說這366人中存有真愛的機率是0.29%，看起來希望渺茫嗎，我看倒未必。

若退一步從二項分配來看，假設真愛只是一個範圍而非唯一，這366人中符合我真愛的人數為隨機變數X，X～B(N=366,P=1/285000) ，直接從期望值來看，才不是我懶得算機率呢，E(X)= 0.001284210526315789，也就是說這366人中只有0.001人是我的真愛，看起來還是略嫌少，但這並不能阻止我繼續算下去。

若再退一步來看，若N→∞，且P→0 (實務上為N>100, NP≤10)，將遇見真愛視為發生機率極小的偶發事件，則可用Poison分配計算近似值。

因此，

X～B(N=366,P=1/285000)→Poi(λ=np=366*1/285000)

則遇見真愛的機率為：

P(x=1)=fx(0)=[ e^-(3661/285000)(366*1/285000)^1 ]/1!

=0.9987166137191

也就是說，要轉角遇到愛了。